Luego de observar varias lluvias de meteoros mayores, es posible de que se encuentre contagiado de la necesidad de “observar-meteoros” y se pregunte si existe algo interesante de observar entre las lluvias de menor actividad. La respuesta es sí, ya que existen lluvias de meteoros llamadas menores las cuales no se han investigado tanto como las mayores. Además de éstas, siempre se pueden observar los meteoros esporádicos. Existe una gran necesidad de observaciones confiables a lo largo del año y si usted tiene algo de experiencia puede contribuir grandemente al entendimiento de todos los diferentes tipos de actividad de meteoros.
No se puede obtener la experiencia necesaria estando sentado dentro de su casa hablando de meteoros. Lea este capítulo cuidadosamente y después salga a observar de forma regular aún si hay frío o le resulte inicialmente algo incómodo. De esta forma pronto pertenecerá al grupo de personas que observan a través del año y gana experiencia para observar de forma correcta las lluvias menores.
Características de observaciones de lluvias menores
Se les llama a las lluvias de meteoros menores debido a que en estas se produce poca actividad para el observador visual. Generalmente se define una lluvia como menor aquella en la cual su tasa por hora (HR Hourly Rate) es menor de 10. Es de admitirse que es un límite arbitrario, pero es de utilidad para nuestros propósitos.
No tiene sentido definir el límite distinguiendo entre lluvia mayor/menor utilizando el ZHR (zenithal hourly rate en inglés, THZ ó tasa horaria cenital en español). La técnica de observación descrita aquí es la apropiada cuando la cantidad observada de meteoros no exceda un cierto límite, ya que este método nos da un cierto tiempo muerto de observación. Es claro que la perdida de tiempo no ha de ser significativa comprometiendo la certeza de la observación. Se ha dicho anteriormente, la meta principal de la observación visual es la confiabilidad de los parámetros físicos de la lluvia. Por lo tanto, consideramos aquellas lluvias que proporcionen menos de 10 meteoros/hora como menores. El trazar en estas lluvias se considera un método esencial de observación.
Esto significa el número visible de meteoros durante una observación es considerablemente menor al de una lluvia mayor. Esta baja actividad meteórica causa problemas específicos los cuales trataremos ahora. En realidad, los periodos de actividad inicial y final de lluvias mayores pueden ser consideradas en efecto lluvias menores, conllevando los mismos problemas.
La actividad esporádica ocurre a través de todo el año. Las trayectorias en el cielo de meteoros esporádicos parecieran estar distribuidos de forma aleatoria. Y, ocurre a veces que al trazar la trayectoria de un meteoro esporádico se cruce accidentalmente con el radiante de una lluvia. Por lo tanto, la información registrada de una lluvia puede contener algunos meteoros esporádicos no pertenecientes a esta. A este efecto se le llama “polución por meteoros esporádicos” y se encuentra en el borde de 1 a 2 meteoros por hora (m/h).
Imagínese una polución esporádica de 2m/h. Al observar una lluvia mayor de unos 80 meteoros por hora, el error relativo sería de solo 2.5%, pero en una lluvia menor de 4 meteoros por hora llegaría a ser de un 50%. Por consiguiente, la polución por meteoros esporádicos es el mayor problema al observar lluvias menores. Si deseamos obtener resultados confiables debemos reducirlo. En las siguientes partes aprenderá a lograr esto.
Enseguida apreciará que esto requiere bastante conocimiento y experiencia. Se necesitarán muchas horas de observación para lograr obtener este talento. Se preguntará entonces si todos los resultados que obtuvieron en esta etapa de aprendizaje no tienen valor. En lo más mínimo. Mientras usted crea que la información que obtuvo de lluvias menores no es completamente confiable, reporte únicamente la cantidad de meteoros vistos. En la tabla “Número de meteoros observados por período y por lluvia” solo apunte en la columna “Tot” y en la tabla “Distribución de Magnitud” solamente anote el total de la distribución de la magnitud. Esta información sobre el total de actividad puede ser utilizada para algunos análisis.
De esta forma podrá aprender paso a paso, sin la presión de reportar gran cantidad de datos de forma correcta. En esta fase de aprendizaje trate de trazar los meteoros, reportar todos los datos, y asignar los meteoros a las diferentes lluvias hasta que usted estime que su información puede considerarse confiable.
Puede darse el caso que usted no quiera llegar tan lejos en la observación de meteoros. Si este es el caso, trate de trazar los meteoros que mira utilizando el método descrito en el capítulo 7 y envíe los datos registrados y mapas al director para observaciones visuales de la Organización Internacional de Meteoros, IMO. Esto implica que no tendrá que pelear con los problemas de observaciones de lluvias menores, pero que su información será de utilidad científica.
Escogiendo el campo de observación
Muchos meteoros son vistos en el centro del campo de visión. Por ende, es importante el escoger el centro del campo como aquel en el que los meteoros que aparecen allí puede ser distinguidos de los esporádicos y asociarse a una lluvia en estudio en ese momento.
En las vecindades del radiante, los meteoros pertenecientes a una lluvia, se mueven lentamente y tienen recorridos cortos mientras que a distancias mas largas del radiante, se asemejan a los esporádicos. Un campo cerca del radiante, aparenta ser más favorable. Como vimos en la sección 6.1, el principal criterio, la dirección del recorrido, también aplica de manera más exacta a meteoros en la vecindad del radiante.
Por lo anterior, uno puede tal vez concluir que es mejor mirar directamente al radiante. Pero debemos de considerar otro punto también. ¿Que propiedad distingue a los meteoros de las estrellas? Su movimiento. Nosotros vemos meteoros débiles entre los cientos de estrellas en nuestro campo, debido a su movimiento Si una estrella débil apareciese durante un segundo no nos daríamos cuenta. ¡Pero este es exactamente el escenario que sucede cuando un meteoro surge en la vecindad inmediata del radiante! Necesitamos un ángulo de movimiento cuando se avista un meteoro. Por otro lado, los meteoros muy rápidos, también no se ven. La velocidad intermedia es óptima para la percepción.
Tomando en consideración todos los factores discutidos anteriormente, una distancia del centro del campo de visión al radiante(s) en estudio de 20° a 40° es ideal. Las distancias de más de 50° deben evitarse.
Además, una elevación de 50° a 70° del horizonte y una distancia del radiante de 20° a 40° , existe un punto adicional para tomar en cuenta. Si va a observar varias lluvias al mismo tiempo, lo cual es perfectamente posible, debe de tomar en consideración que los radiantes no se sitúen en una línea como es visto desde el centro del campo. De otra forma, los meteoros de estos radiantes no podrán ser distinguidos por las direcciones de sus recorridos y distinguirlos por su velocidad angular o únicamente por la longitud de su recorrido será más difícil y menos certero.
Al observar, por ejemplo, las Oriónidas con su radiante cerca de Betelgeuse (beta Ori) y las epsilon Gemínidas con su radiante cerca de Pollux (beta Gem) el centro del campo debería estar en Tauro/Auriga/Perseo o Can Mayor/Monoceros/Can Menor más bien que en Cáncer/Osa Mayor o Liebre/Eridano.
Cuando haya escogido el campo mejor situado, debería de seguir su movimiento diurno mientras las condiciones lo permitan (elevación del campo de 50° -70° , luces artificiales, obstrucciones, etc.). Si usted se ve en la necesidad de cambiar de campo, anote el tiempo de este cambio y el nuevo campo. Para el análisis, el tiempo de dicho cambio debería de ser idéntico al límite del intervalo de observación.
Observando el meteoro
Cuando aparezca un meteoro, mantenga su mente alerta. Trate de guardar el fenómeno completo en su memoria. Luego siga viendo el cielo para memorizar la siguiente información (en este orden):
- El recorrido:
La información más importante es su dirección antes que sus puntos exactos de inicio y fin. Memorícelo de acuerdo a las estrellas de fondo, es decir entre cuales estrellas paso el meteoro o entre cuales puede ser rastreada nuevamente o prolongada. - Magnitud máxima:
Estime ésta comparándola con la brillantez de las estrellas vecinas que memorizó al principio de la observación. - Velocidad Angular:
Para tener una cantidad que pueda compararse con un valor esperado para asociar una lluvia, usted debe de estimar ésta en grados por segundo. Esto no es complicado. En su imaginación, usted supone que un meteoro se mueva por un segundo. El lapso de tiempo de un segundo puede ser reproducido fácilmente y la sensación de la velocidad angular, aun la tiene en la memoria. La longitud del recorrido en grados que el meteoro haya alcanzado después de moverse por un segundo, es su velocidad angular en grados por segundo. Una vez se tenga mas experiencia, usted tendrá la escala fija en su memoria y puede entonces estimar la velocidad angular directamente sin utilizar este procedimiento. No intente de estimar la duración y de obtener la velocidad angular dividiendo su longitud del recorrido entre su duración. La duración es muy difícil e incierta para estimar y la longitud del recorrido es afectada por trazar errores, por lo que el resultado incierto de la velocidad angular es mucho mayor que si convirtiera la sensación de la velocidad directamente en grados por segundo. Los gráficos dan una idea acerca de la precisión que logran los observadores experimentados.
- Estela persistente:
Indique su duración en segundos. Las estelas muy cortas pueden marcarse con una “+”. Las estelas de larga duracion de meteoros brillantes pueden mostrar comportamientos interesantes de atenuación. Las mismas pueden resultar dobladas o distorsionadas, y usted debe de anotar los detalles de estos fenómenos. - Color:
Note que generalmente es imposible detectar colores en meteoros menores a magnitud +2. Este dato es el de menor valor de toda la información.
Ahora, usted puede escoger la carta en donde el meteoro se ha trazado mejor, es decir aquella carta estelar en la cual el meteoro se encuentra lo mas cerca del centro. Vale la pena preparar un surtido de cartas para que usted sepa la secuencia exactamente y pueda encontrar la tarjeta más adecuada y no interrumpir la observación. El siguiente paso es la identificación de las estrellas que utilizó para memorizar el recorrido en la propia carta. Ya que las cartas contienen todas las estrellas hasta la magnitud +6.5 usted debería de encontrarlas fácilmente a menos que su limite de magnitud es considerablemente mejor que +6.5mag. Este paso es una fuente para trazar errores, por lo que ¡hay que tener cuidado! Si usted está seguro que ha encontrado las estrellas correctas, puede trazar el meteoro de memoria. Para identificación, el trazo debe de numerarse.
Finalmente, usted debe de estimar la precisión del trazo con la siguiente escala:
- Muy preciso
- Precisión intermedia
- Precisión pobre
Para sus primeras observaciones, el trazo requerirá de algún tiempo. No se apure: tome su tiempo para trazar con cuidado. ¡Lo mas importante es la calidad! El tiempo necesario para trazar reducirá rápidamente con la experiencia. Los observadores expertos necesitan un promedio de 10 a 30 segundos.
Después de trazar, vea su reloj para registrar la hora. A menos que haya visto un bólido, la hora debe de ser aproximada unicamente. Una exactitud de un minuto es suficiente. Luego debe de registrarse todo el resto de la información. Puede completar una lista como se indica en la figura de abajo.
Para poder ahorrar tiempo de observación, se puede registrar la información en cinta magnética. En esta caso usted debe lenar la lista después de la observación. Para meteoros trazados necesitará cierto tiempo, durante el cual debe ver a sus tarjetas en vez de al cielo. Por lo tanto, el tiempo de observación efectivo debe reducirse por el tiempo de trazo. Seria un esfuerzo mayor el registrar el tiempo que se utilizó en trazar cada meteoro individualmente, por lo que es mejor determinar el tiempo promedio para trazar un meteoro como se indica a continuación.
Utilice un cronómetro que pueda sumar tiempos. Cuando empiece a ver la tarjeta inicie el cronómetro para trazar, deténgalo al finalizar el trazo en, digamos 38.4 s (0:38.4), cuando ocurra el siguiente meteoro después de algunos minutos, inicie otra vez a los 38.4s, deténgalo después del trazo a 1:22.6 y así sucesivamente. Después de observar un dado número de meteoros, digamos 25, el cronómetro despliega el tiempo en el que usted no observó el cielo, digamos 16 min 40 s. Dividiendo este tiempo entre 25 meteoros, obtendrá un promedio de tiempo de trazo de 40 s por meteoro (16 min 40 s = 1000 s, 1000 s / 25 meteoros = 40 s / meteoro). Si usted observó, por ejemplo 29 meteoros en un intervalo, el tiempo total de trazo a ser restado del tiempo efectivo es 29 meteoros por 40 s/meteoro = 1160 s = 19m 20s ~19 min. En la forma de reporte (análisis de intervalos) estas cantidades deben de ser llenadas en la línea “Tiempo para trazo ______ s / meteoro, _________min total”. Para los observadores experimentados el tiempo promedio para trazar un meteoro es una constante que debe revisarse unas dos veces al año a traves del procedimiento descrito con anterioridad. Los novatos deben revisarlo regularmente, digamos cada tres observaciones de meteoros.
Criterio para asociación de una lluvia
Generalmente las partículas en un enjambre de meteoroides se mueven en órbitas similares y por lo tanto entran a la atmósfera de forma paralela entre ellas y a prácticamente la misma velocidad, generando de ese modo una lluvia de meteoros. Esto brinda ciertas características muy útiles para poderlas distinguir de otros meteoros que no pertenecen a esa lluvia.
Radiante y trayectoria
Como usted conoce las Observaciones de Lluvias importantes las lluvias de meteoros parecen proceder de un punto en el cielo llamado radiante. Para ganar un poco de conocimientos en este tema, vayan a las Figuras 1 y 2 las cuales enseñan como los observadores A, B, C, D y E proyectan un meteoro M hacia el hemisferio estelar, como secciones de arco. Estos grandes círculos, atañen a los meteoros que pertenecen al mismo radiante y que tienen dos polos o puntos de intersección en común: el radiante R arriba del horizonte y el anti radiante AR abajo. El plano perpendicular a los grandes círculos a través de O, marca los puntos a una distancia de 90° desde el radiante.
Cuando el centro de la carta P se sitúa a menos de 90° del radiante, puede ser marcado en el mismo plano que del mapa utilizando la formula de proyección usual. Las extensiones hacia atrás de los de los meteoros de la lluvia, están en el radiante. Para su conveniencia, el Calendario de Lluvias incluye una tabla indicando las posiciones y la dirección de los radiantes.
Cuando un radiante está a más de 90° del centro del mapa, no puede ser proyectado en la carta, pero si el anti radiante. Su posición resulta de:
delta_AR = – delta_R
alpha_AR = alpha_R ± 180°
Ahora, la prolongación del trazo del meteoro cumple el anti radiante. Esto también se vuelve obvio de la Figura 2.
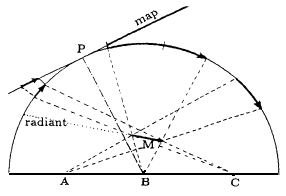Figura 1 – Vista de lado de la trayectoria proyectada en la esfera celeste y en el mapa. P denota el centro del mapa (centro de la proyección) y M es la trayectoria del meteoro
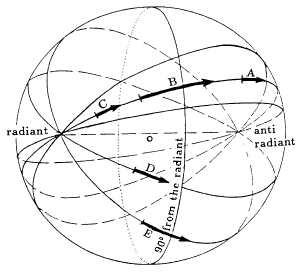Figura 2 – Vista de la esfera en la cual la trayectoria del meteoro es proyectada de diferentes lugares. . A, B y C se sitúan en el mismo meridiano (círculo grande). Otros observadores (D, E) pueden verlo en otros círculos grandes.Debido a perturbaciones y diferentes condiciones de emisión de su cuerpo progenitor, las partículas individuales de una lluvia de meteoros no se mueven exactamente en la misma orbita. Por ello, no entran a la atmósfera exactamente paralelamente una de otra. El resultado es que el radiante no es un punto, sino un área de cierto tamaño cuyas dimensiones dependen en como se esparcen las orbitas individuales, y en las condiciones geométricas de cómo el enjambre encuentra a la Tierra, por lo que además, difiere de lluvia a lluvia (Kresák & Porubcan, 1970)
Si usted traza lluvias de meteoros, sus extensiones hacia atrás formarán el área del radiante considerablemente mayor al radio obtenido de observaciones fotográficas. Esto es debido a errores en el trazo. Estos errores se reducen al tener más experiencia en las observaciones, pero generalmente no pueden evitarse. Al decidir si un meteoro pertenece a una lluvia o no, la pregunta que resulta es que tan seguramente podemos asumir el área del radiante. Haciéndola muy grande, implica que la polución de esporádicos se vuelve muy grande. Es decir varios meteoros esporádicos serán parte del radiante de una forma accidental. Si el área del radiante es muy pequeña, una cantidad pequeña de meteoros serán clasificados como esporádicos por problemas de trazo. Los diámetros óptimos de los radiantes para asociación de lluvias son dados en la Tabla 6 y 7
Velocidad angular
Los meteoros de una lluvia específica comienzan a emitir luz a alturas similares arriba de la superficie de la Tierra. Sus velocidades también son similares, con pocas diferencias. La desaceleración de su trazo luminoso a través de la atmósfera puede ser confundida por meteoros ordinarios; su velocidad es reducida en un porcentaje únicamente. Para nuestros propósitos podemos asumir que los meteoros de lluvias se mueven paralelamente con una velocidad constante.
Hasta ahora, la velocidad angular aparente (w) de un meteoro perteneciente a una lluvia (en grados por segundo) puede ser calculado por la fórmula indicada abajo dependiente de su velocidad preatmosférica V_infty (km/s), la elevación h_b (grados) y la altitud H_b (km) de su punto de partida, y la distancia angular entre su punto final y el radiante D_e (grados).
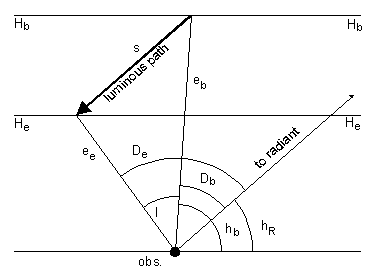
Donde l es la longitud aparente del trazo del meteoro y s es su longitud real de su trazo.
Para longitudes de trazos aparentes l menores que ~30° encontramos:
l / sen l ~ constante + 1 rad ~57.3°
Finalmente podemos escribir:
La velocidad angular omega de un meteoro de lluvia es por lo tanto bien definido de cualquier punto en el cielo. Es un criterio estricto utilizado para la asociación de lluvias.
En la tabla de abajo, se han calculado las velocidades angulares omega por cada diferente velocidad de entrada V. Debido a que altitud inicial H_b depende principalmente de V, se han asumido en los cálculos las altitudes iniciales características para velocidades geocéntricas individuales.
La siguiente tabla es utilizada para determinar la velocidad angular esperada de meteoros pertenecientes a una lluvia. Para la interpolación de los valores no incluidos directamente en la tabla, por favor vaya a los ejemplos indicados debajo de la tabla.
Tabla 1. Velocidad angular omega (en grados) como función de la elevación del punto de inicio de un meteoro (h_b) y la distancia angular (D_e) entre el punto final y el radiante, para valores varios de la velocidad geocéntrica de la corriente V. H+b es la altitud de el punto de inicio del meteoro arriba de la superficie de la Tierra.
V=20 km/s H_b=100 km | V=25 km/s H_b=100 km
h_b= 10° 20° 40° 60° 90° | 10° 20° 40° 60° 90°
|
D= 5° 0.2 0.3 0.6 0.9 1.0 | 0.2 0.4 0.8 1.1 1.3
10° 0.3 0.7 1.3 1.7 2.0 | 0.4 0.9 1.6 2.2 2.5
20° 0.7 1.3 2.5 3.4 3.9 | 0.9 1.7 3.2 4.3 4.9
40° 1.3 2.5 4.7 6.3 7.3 | 1.6 3.2 5.9 8.0 9.3
60° 1.7 3.4 6.3 8.5 9.8 | 2.2 4.3 8.0 11 13
90° 2.0 3.9 7.3 9.8 11 | 2.5 4.9 9.3 13 14
V=30 km/s H_b=100 km | V=35 km/s H_b=100 km
h_b= 10° 20° 40° 60° 90° | 10° 20° 40° 60° 90°
|
D= 5° 0.3 0.5 1.0 1.4 1.6 | 0.3 0.6 1.1 1.5 1.7
10° 0.5 1.1 2.0 2.7 3.1 | 0.6 1.2 2.2 3.0 3.4
20° 1.1 2.1 4.0 5.3 6.2 | 1.2 2.3 4.3 5.8 6.7
40° 2.0 4.0 7.4 10 12 | 2.2 4.3 8.2 11 13
60° 2.7 5.3 10 14 16 | 3.0 5.8 11 15 17
90° 3.1 6.2 12 16 18 | 3.4 6.7 13 17 20
V=40 km/s H_b=100 km | V=50 km/s H_b=110 km
h_b= 10° 20° 40° 60° 90° | 10° 20° 40° 60° 90°
|
D= 5° 0.3 0.7 1.3 1.7 2.0 | 0.4 0.8 1.5 2.0 2.3
10° 0.7 1.4 2.6 3.5 4.0 | 0.8 1.6 2.9 3.9 4.6
20° 1.4 2.7 5.0 6.8 7.9 | 1.6 3.1 5.8 7.8 9.0
40° 2.6 5.0 9.5 13 15 | 2.9 5.8 11 15 17
60° 3.5 6.8 13 17 20 | 3.9 7.8 15 20 23
90° 4.0 7.9 15 20 23 | 4.6 9.0 17 23 26
V=60 km/s H_b=115 km | V=66 km/s H_b=115 km
h_b= 10° 20° 40° 60° 90° | 10° 20° 40° 60° 90°
|
D= 5° 0.5 0.9 1.7 2.3 2.6 | 0.5 1.0 1.9 2.5 2.9
10° 0.9 1.8 3.4 4.5 5.2 | 1.0 2.0 3.7 5.0 5.8
20° 1.8 3.5 6.7 9.0 10 | 2.0 3.9 7.3 10 11
40° 3.7 6.7 13 17 20 | 3.7 7.3 14 18 21
60° 4.6 9.0 17 23 26 | 5.0 10 18 25 29
90° 5.3 10 20 26 30 | 5.8 11 21 29 33
V=70 km/s H_b=126 km
h_b= 10° 20° 40° 60° 90°
D= 5° 0.5 0.9 1.8 2.4 2.8
10° 1.0 1.9 3.6 4.8 5.5
20° 1.9 3.7 7.0 9.4 11
40° 3.6 7.0 13 18 21
60° 4.8 9.4 18 24 28
90° 5.5 11 21 28 32
Examples:
1. Virginid V=35 km/s h_b=60° D_e=40° omega=11°/s
2. Orionid V=66 km/s h_b=30° D_e=60° omega~14°/s
3. Ursid V=33 km/s h_b=50° D_e=30° omega~ 7°/s
Longitud aparente de la trayectoria
Asumiendo altitudes constantes de inicio y fin (H_b, H_e) para meteoros pertenecientes a cierta lluvia, se puede calcular la longitud aparente del trazo esperada l para miembros de la lluvia dependiendo de la elevación del radiante (h_R), la elevación del punto de inicio (h_b) y la distancia angular entre el radiante y el punto de inicio (D_b):
Para altitudes dadas de inicio y fin, l depende de tres cantidades: h_R, h_b y D_b. Para visualizar esta dependencia, deberíamos construir un diagrama de 4 dimensiones, lo cual es imposible. Esto significa que el criterio es muy difícil de manejar. Pero, calculando l por diferentes combinaciones de altitudes de inicio/fin, se encuentra:
D_b / l ~ constante para D_b <30°
Esto significa que el criterio l puede ser utilizado favorablemente en la vecindad del radiante. En esta región, los meteoros perecientes a una lluvia se distinguen de los esporádicos por sus trazos cortos. Tomando en cuenta que la altitud final depende de la masa de la partícula y del material que la compone, es oportuno asumir que l es considerada el límite superior de la pertenencia de una lluvia. Hasta ahora se asumía que H_b = 100km y H_e = 80km. El resultado se muestra en la Figura 4.
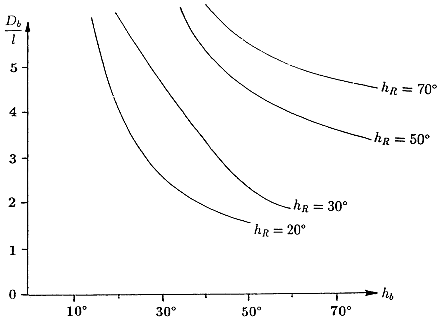Figura 4 – El cociente D_b / l para D_b <30° como una función de h_b para varias elevaciones del radiante h_R Los calculos fueron realizados utilizando H_b = 100 km, y H_e = 80kmPuede darse que los radiantes que tengan poca elevación produzcan trazos meteóricos largos (valor pequeño de D_b / l) Cuanto más alto aparezca un meteoro en el cielo más cerca estará del observador, y por ende, la longitud del trazo se verá través de un ángulo mayor (longitud de trazo aparente l). La aplicación de las cantidades ilustradas en la Figura 4 para asociación de lluvias, es problemática ya que las altitudes finales pueden variar grandemente y la longitud del trazo sale mucho mas afectada trazando errores que en la dirección. Por lo que solo podemos establecer una regla general:
Para radiantes que se encuentran a una altura mayor que 30° , la longitud del trazo aparente l de un meteoro perteneciente a una lluvia totaliza casi la mitad de la distancia del radiante al punto de inicio.
Consecuentemente, la distancia entre el radiante y el punto de inicio de un meteoro trazado en la carta, debe de ser por lo menos el doble de largo que el trazo del meteoro en si, si se sospecha que el meteoro pertenece a una lluvia. Esta regla no es valida para bólidos los que generalmente penetran mas profundo en la atmósfera y por ende producen trazos más largos.
Revisando la Figura 4, la formulación de la regla aparenta ser bastante débil, ya que los factores de 3-5 serían válidos para muchos meteoros, pero si se fortalece la regla, existe el peligro de clasificar un numero considerable de meteoros de lluvia en las vecindades del radiante como esporádicas, debido a trayectorias cortas que se trazan como muy largas. La experiencia indica que un factor de dos es considerablemente suficiente para distinguir meteoros esporádicos cumpliendo con el criterio de dirección de trazo y velocidad angular, entre algunos límites de error, de meteoros reales pertenecientes a lluvias.
Analysis
En la seccion “Criterio para asociación de una lluvia”, usted aprendió acerca de los criterios que un meteoro debe de cumplir para que pueda ser considerado como un miembro altamente probable de una lluvia. Ahora, se estudiará el uso práctico de los criterios. Una tarde libre debería ser suficiente para analizar la observación.
Primero, tome la lista de trabajo de la IMO de lluvias de meteoros y selecione todas las lluvias activas en la fecha de su observación. Luego trace, en las cartas, las posiciones de sus radiantes válidas para dicha fecha. Tome en consideración el movimiento de los radiantes utilizando la tabla para dicho propósito.
Tabla 2. Límites de error para la velocidad angular (w) a asumirse en la asociación de la lluvia.
Velocidad angular [°/s] 5 10 15 20 30 Error permitido [°/s] 3 5 6 7 8
Tabla 3. Diámetros óptimos de radiante a ser asumidos para la asociación de lluvias de meteoros menores para definir correcta y moderadamente los radiantes definidos como una función de la distancia del meteoro hacia el radiante.
Distancia radiante Diámetro optimo del
Del meteoro [° ] radiante [° ]
15 14
30 17
50 20
70 23
Tabla 4. Tamaños óptimos de los radiantes en ascensión recta (a) y declinación (d) para asumir en la asociación de lluvias de radiantes complejos.
Radiante distancia del meteoro 15° 30° 50° 70° delta-Cancridas (DCA) 20°/13° 24°/18° 26°/21° 34°/30° Virginidas (VIR) 30°/20° 31°/23° 33°/26° 40°/34° Sagitaridas (SAG) 30°/20° 31°/23° 33°/26° 40°/34° Tauridas del Sur (STA) 20°/13° 24°/18° 26°/21 34°/30° Tauridas del Norte (NTA) 20°/13° 24°/18° 26°/21° 34°/30° Puppidas (PUP) 20° 24° 26° 34°
Los diámetros de los radiantes obtenidos en la sección anterior son trazados como círculos concéntricos (o elipses para los radiantes complejos) en la carta (ver Tablas 3 y 4). La escala no es constante en la carta. Por lo tanto, un radiante de 20° de diámetro en el centro de la carta, aparece más pequeño que uno del mismo diámetro cerca de borde de la carta. La Tabla 5 nos muestra la variación de escala a través de la carta. Como un ejemplo, un radiante de de 20° de diámetro a 150mm de distancia del centro de la carta, aparece como un círculo de 104mm de diámetro.
Tabla 5. La escala s está en mm/° para diferentes distancias d al centro de las cartas gnomónicas del Atlas Brno (válido para el radio de proyección original R = 160.43 mm).
d [mm] 0 50 100 120 150 170 200 220 s [mm/° ] 2.8 3.1 3.9 4.4 5.2 5.9 7.1 8.1
Después de trazar los radiantes en las cartas, usted debe de analizar cada meteoro de forma separada. Utilice una regla de por lo menos 30cm de longitud para extender el trazo hacia atrás del meteoro. Si la extensión hacia atrás cumple con el área del radiante del tamaño correspondiente, el meteoro puede pertenecer a esta lluvia, es decir, la condición necesaria para que el camino pueda ser extendido hacia atrás al radiante, debe cumplirse. Puede suceder que un meteoro pertenezca a un radiante que esta siendo trazado en una carta vecina. La extensión hacia atrás es prolongada en esta otra carta utilizando estrellas que estén presentes en ambas cartas, es decir, estrellas en la región de traslape. Usted debe de identificar las estrellas cruzadas o que pasen cerca de la línea de la carta vecina y trazar la línea en la posición correspondiente a estas estrellas en la segunda carta.
En el siguiente paso, analizaremos la condición que la longitud del camino debe ser menor que la mitad de la distancia angular del radiante al punto de inicio. Debido a que esto es únicamente una medida muy tosca podemos descuidar la escala variable de la carta. Las distancias son medidas utilizando una regla y comparadas. Si la condición de cumple, podemos revisar la siguiente condición.
La velocidad angular debe corresponder al valor esperado entre los limites de error indicados en la Tabla 2. Para revisar esta condición, usted necesita un planisferio válido para latitud de su sitio de observación, para determinar la elevación del punto de inicio del meteoro y la Tabla 1. Además de la elevación de inicio, usted debe de determinar la distancia angular entre el radiante y el punto final del meteoro.
Usted puede estimar la distancia del radiante en el planisferio, con suficiente precisión. Alternadamente, estime la distancia del meteoro al radiante, comparando con las distancias entre estrellas, tal y como se presenta en la siguiente tabla.
Table 6. Distancias entre estrellas brillantes como se indica en las cartas del Atlas Brno. Las distancias son redondeadas en incrementos de 5 grados.
Carta 1 alpha Per -- alpha Aur 20 Carta 5 alpha Boo -- alpha CrB 20
alpha Per -- alpha UMi 40 alpha Boo -- alpha Vir 35
alpha Per -- alpha Cyg 60 alpha Vir -- eta UMa 60
Carta 2 alpha UMa -- eta UMa 25 Carta 6 eps Peg -- alpha Aql 30
alpha UMi -- alpha Aur 45 alpha Aql -- alpha Cyg 40
alpha Gem -- beta Leo 60 alpha And -- alpha Aql 65
alpha UMi -- beta Leo 75
Carta 7 alpha Tau -- Pleiades 15
Carta 3 alpha UMi -- beta UMi 15 alpha And -- beta Cet 50
alpha Cyg -- alpha Lyr 25 alpha And -- alpha Tau 60
alpha Lyr -- alpha CrB 40
alpha Cyg -- eta UMa 65 Carta 8 alpha Leo -- beta Leo 20
alpha Leo -- alpha CMi 35
Carta 4 alpha Gem -- beta Gem 5 beta Crv -- beta Gem 85
alpha Ori -- beta Ori 20
alpha Tau -- alpha CMi 45 Carta 9 alpha CrB -- alpha Her 25
alpha Aur -- alpha Ori 55 alpha Aql -- alpha Her 40
alpha Aql -- alpha Sco 60
Luego, determine la elevación del punto de inicio utilizando el planisferio. Ahora tome la Tabla 1 y determine la velocidad angular esperada de acuerdo a la velocidad geocéntrica de entrada V, la distancia del radiante D y la elevación h_b que acaba de obtener. Este valor debe compararse al que usted estimó durante la observación. Si la diferencia está entre los límites de error permisibles la condición de velocidad angular ha sido cumplida. Los límites de error a ser utilizados se muestran en la Tabla 2. La tabla debe de leerse como en este ejemplo. Si la velocidad angular se considera debe de ser 15°/s, la condición se cumple si el valor estimado está en el rango de 9-21°/s.
Si el meteoro cumple con los tres criterios, puede considerarse como un miembro de la lluvia. Hay veces que puede suceder que un meteoro cumple con las condiciones de pertenencia a dos lluvias diferentes. En este caso, usted debe de escoger la lluvia más probable, es decir, aquella cuyas condiciones se cumplan mejor. Es imposible considerar que un meteoro sea miembro de dos o más diferentes lluvias. Usted debe decidir a favor de una lluvia, incluso si la probabilidad de que un meteoro pertenezca a dos lluvias es similar.